
在浏览振动试验机的产品目录时,同一台设备,可以看到随机推力最大有效值一般都在正弦最大推力的80%附近。另外,在计算随机推力的时候,一般厂家都会推荐随机加速度的有效值控制在正弦最大加速度的1/3以下。下面个人就对这两句话的理解,进行说明。
正弦振动试验
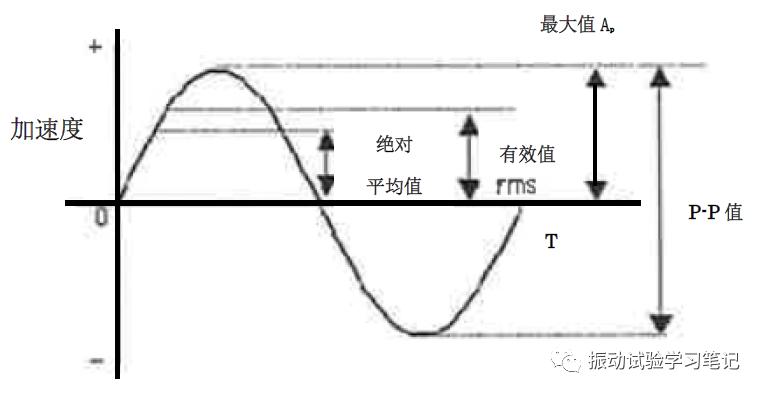
当初相位为零的时候,其函数式可以表示为,
A(t)= Ap sin(ωt)
其中,Ap为正弦加速度最大值,角速度ω =2π/T。对应一个周期(T)的
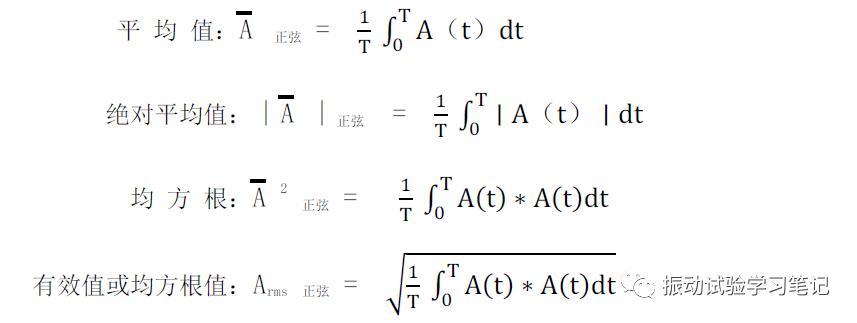
函数式代入,通过积分计算得到(计算结果适用于整个正弦试验过程),

随机振动试验
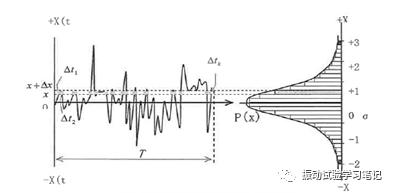
假设随机振动是一个平稳的、遍历的和满足正态分布的过程,一般随机振动的位移平均值为0,所以其位移的概率密度函数为,

p(x)---振动位移幅值概率密度函数,
x---位移瞬时幅值
ρ---位移标准偏差
随机振动位移的产生是由振动控制仪通过内部的计算产生,对应的加速度和速度也可以理解为符合正态分布,所以加速度的概率密度函数为
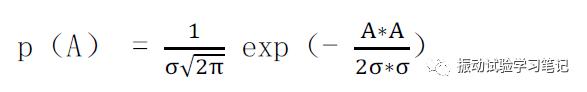
p(A)---振动加速度幅值概率密度函数,
A---加速度瞬时幅值
σ---加速度标准偏差
通过加速度的概率密度函数可以计算随机振动加速度的

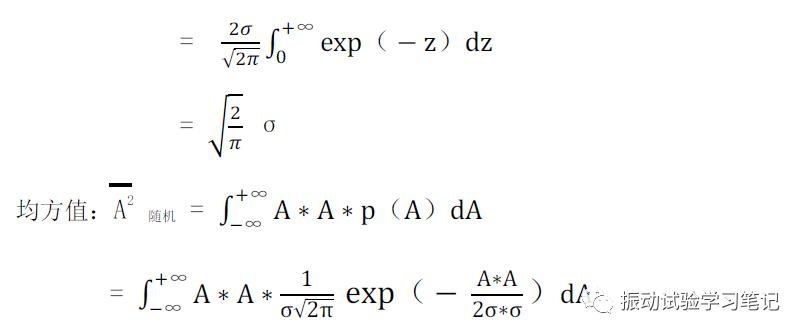


其实,随机的绝对平均值和正弦的绝对平均值是可以同样看待的,两者相等即表示振动的能量相同。于是可以得到,

上式中可以看出,当正弦最大加速度为Ap时,对应的随机振动加速度有效值为其的80%。通过牛顿第二定律,可以计算出随机推力最大有效值一般都在正弦最大推力的80%附近。
接下来,我们来理解在计算随机试验推力的时候,随机加速度的有效值控制在正弦最大加速度的1/3以下这句话。因为随机振动时控制仪产生的加速度符合正态分布,μ为加速度平均值(一般μ= 0),σ为加速度标准方差,也就是加速度有效值(均方根值Arms随机)。
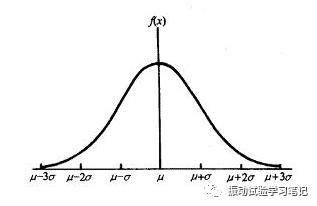
通过计算我们可以知道,随机加速度落在±σ范围内的概率是68.27%,在±2σ内的概率是95.45%,在±3σ内的概率是99.73%,σ对应的系数1、2、3…就是控制仪里面的削波系数。所以,当通过PSD计算出随机加速度有效值后,实际在试验中产生的瞬时加速度为有效值的±3倍(偶尔也会±5~6倍,负值代表反方向)。这就是计算推力时,随机加速度的有效值控制在正弦最大加速度的1/3以下的由来,当然削波系数设定为3。当有效值较小的时候,削波系数可以使用控制仪中的默认值。
综上所述,在随机试验计算推力的时候,主要还是需要考虑有效值,尽量将加速度有效值控制在正弦最大加速度的1/3以下,也就是说当试验机的正弦最大加速度为1000m/s2时,其对应的随机加速度有效值最大333.3m/s2,即随机试验对应的最大有效推力是正弦试验最大推力的1/3。这是一个最保险的方法,一般不会损坏振动试验机。

备注:图片和部分文字等来源于网络,如有侵权,请联系作者本人。

长按二维码识别关注我们
