еңЁmatlabдёӯпјҢжҲ‘们用дёӨз§Қж–№ејҸеҺ»жұӮи§ЈPDEж–№зЁӢпјҢдёҖз§ҚжҳҜдҪҝз”Ё PDE toolboxпјҢеҸҜд»ҘеңЁAppдёӯжҹҘжүҫеҲ°PDE ModelerпјҢ然еҗҺжү“ејҖпјҢйҖҡиҝҮз»ҳеҲ¶еӣҫеҪўпјҢи®ҫзҪ®иҫ№з•ҢпјҢйҖүжӢ©ж–№зЁӢе’Ңз»ҶеҢ–зҪ‘ж јпјҢ然еҗҺжұӮи§ЈеҮәз»“жһңпјӣеҸҰеӨ–дёҖз§ҚжҳҜйҖҡиҝҮзј–иҜ‘д»Јз ҒпјҢиҝҗз”ЁFunctionеҮҪж•°иҝӣиЎҢжұӮи§ЈпјҢзҺ°еңЁжҲ‘们е°ұе°қиҜ•з¬¬дәҢз§Қж–№жі•е®һзҺ°з”өиҠҜзғӯд»ҝзңҹиҝҮзЁӢгҖӮ
еңҶжҹұз”өжұ зғӯжЁЎеһӢ
жҲ‘д»¬ж №жҚ®еңҶжҹұзҡ„дә§зғӯе’Ңж•Јзғӯзү№зӮ№пјҢеҸӮиҖғзӣёе…іиө„ж–ҷпјҢе»әз«ӢжЁЎеһӢеҰӮдёӢ

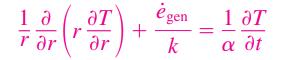
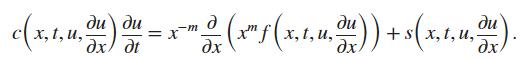
function [c,f,s] = pdex1pde(r,t,u,dudx)global alpha k e_genc = 1/alpha;f = dudx;s = e_gen/k;жӯӨеӨ–еҲқе§ӢжқЎд»¶е’Ңиҫ№з•ҢжқЎд»¶д№ҹеҸҜд»Ҙзӣёе…іеҜ№еә”зҡ„иЎЁиҝ°пјҢеҲҶеҲ«дёәfunction u0 = pdex1ic(r)global Tinitu0 = Tinit;function [pl,ql,pr,qr] = pdex1bc(xl,ul,xr,ur,t)global h k Tinitpl = 0;ql = 1;pr = h*(ur-Tinit);qr = k;
3.жЁЎеһӢи®Ўз®—
и®ҫзҪ®еҲқе§ӢеҖје’Ңз»ҳеҲ¶еӣҫеғҸпјҢзӣёе…ід»Јз ҒеҸӮиҖғе…¶д»–иө„ж–ҷеҰӮдёӢfunction [] = battery(C_rate)global k e_gen Tinit h alphacell_capacity = 1.1;C_rate=2;I = cell_capacity*C_rate;R_int = 0.017;Tinit = 30;V = pi*(0.009)^2*(0.065);k = 0.20;Cp = 1000;rho = 2362;h = 10;alpha = k/(rho*Cp);power = I^2*R_int;e_gen = power/V;total_t = 3600/C_rate;close allfilename = ['battery_' num2str(C_rate) 'C']m = 1;r = linspace(0,0.009,100);t = linspace(0,total_t,100); sol = pdepe(m,@pdex1pde,@pdex1ic,@pdex1bc,r,t);T = sol(:,:,1);pcolor(r.*1000,t./60,T)xlabel('Distance from center, r (mm)')ylabel('Time, t (min)')hcb = colorbar; title(hcb,'Temperature (^oC)')title([num2str(C_rate) 'C'])print(filename,'-dsvg')figureSOC = t.*C_rate/3600*100;y_limits = [29 ceil(max(T(:))+1)];for i = 1:length(T(:,1)) plot(r.*1000,T(i,:)); title(['t = ' num2str(t(i)./60,3) ' min; SOC = ' num2str(SOC(i),3) '%'],'FontSize',16) xlabel('Distance from center, r (mm)') ylabel('Temperature (^oC)') ylim(y_limits) drawnow frame = getframe(2); im = frame2im(frame); [imind,cm] = rgb2ind(im,256); if i == 1 imwrite(imind,cm,[filename '.gif'],'gif','Loopcount',1); else imwrite(imind,cm,[filename '.gif'],'gif','WriteMode','append','DelayTime',0.05); endend4.з»“жһңеҲҶжһҗ
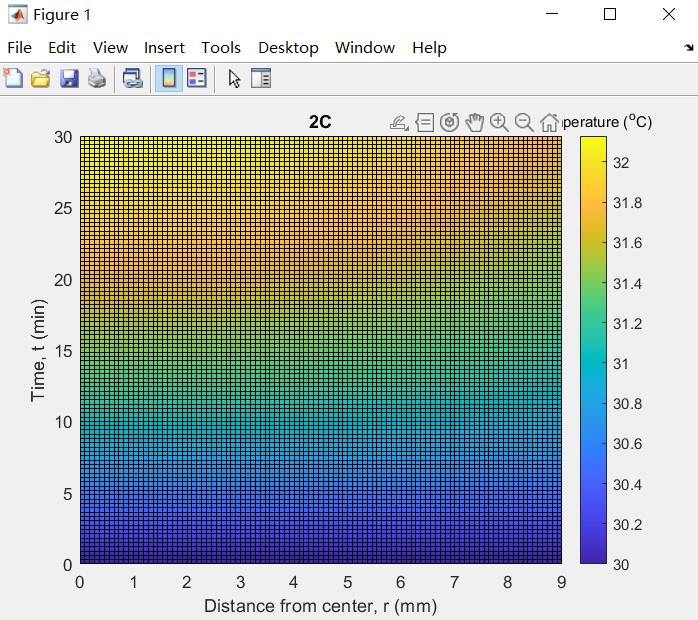
д»ҺдёӢйқўеӣҫзӨәеҸҜд»ҘзңӢеҮәпјҢ30minз”өжұ еҸҜд»ҘиҫҫеҲ°32в„ғгҖӮ