
本文来源于振动试验学习笔记
***时差域(自相关函数、互相关函数)
给出频率成份和时间历程之间的信息。
(1)自相关函数Rxx(τ)(auto-correlation function):反应同一随机信号x(t)在时刻t和(t+τ)时的相互依赖关系,定义为两时刻随机变量的乘积的平均值。
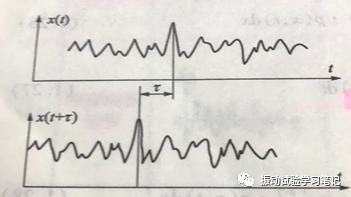
当平均时间趋近于无穷大时,便得到自相关函数,其数学式和曲线如下所示,是时差τ的函数。
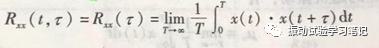
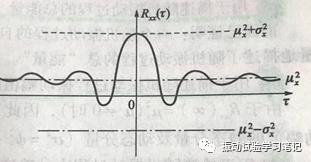
随机振动自相关函数曲线
上图中可以看出,Rxx(τ)越大,同一随机振动信号两时刻的信号相似性越好;Rxx(τ)越小,相似性越差。对于平稳随机振动,当τ趋近于无穷大时,两个信号越来越不相关,且其值趋近于μ2。μ= 0时,其也趋近于零。
随机振动试验中,很重要的一个函数,主要作用如下,
1 用于描述随机振动过程的总能量以及静态分量和动态分量。
当τ= 0的时候,即
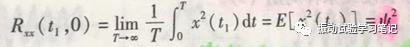
2 用于检测随机振动过程中的确定性周期振动。
它可以把随机信号中的周期成份检测出来。因为任何周期信号在所有的时移上都有一定的自相关函数图形,当在自相关函数图上发现时差τ趋于无穷大,Rxx(∞)≠0,而有某种周期性,即说明随机振动信号中混有周期信号成份。
3 用于构建自功率谱密度函数,通过对自相关函数进行傅里叶变换即可得到,随机振动试验中很重要的一个分析方法,和PSD关系很大。
(2)互相关函数Rxy (τ)(cross-correlationfunction):反应两个随机信号x(t)、y(t)在时刻t和t+τ的相互依赖关系。
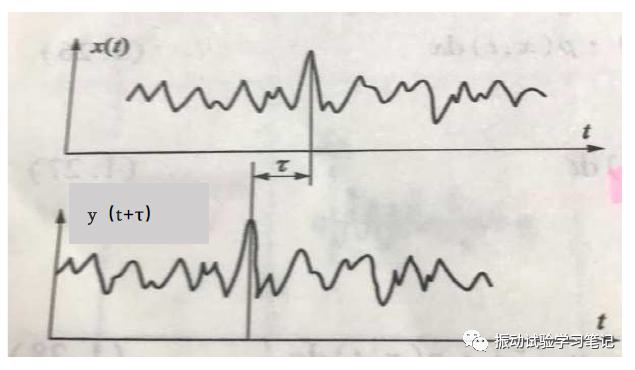
其数学式和曲线如下所示,是时差τ的函数。
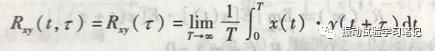

随机振动互相关函数曲线
同样也是一个重要的函数,可以用于检测振动系统响应信号与激励信号的滞后时间,因为信号在系统中的时间滞后值,可以通过输入和输出的互相关函数中的峰值位置来确定,互相关函数最大值偏离坐标中心位置的时间坐标移动值,就是信号通过系统所需时间(图中τ0)。用于确定信号传递通道,如果一线性系统的输入通过几个通道输出,利用互相关函数的时移,可以确定那个通道为主要的。用于辨别随机信号中的成份,用于构建互功率谱密度函数(傅里叶变换)。
***频域(自功率谱密度函数、互功率谱密度函数)
(1)自功率谱密度函数Sxx(ω):将平稳随机振动过程x(t)的自相关函数Rxx(τ)的傅里叶变换定义为随机振动过程的自功率谱密度函数Sxx(ω)。其数学式如下所示,
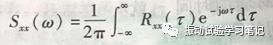
其傅里叶逆变换即
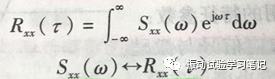
下表列举了各类振动信号的概率密度、自相关、自功率谱等的曲线,供参考。
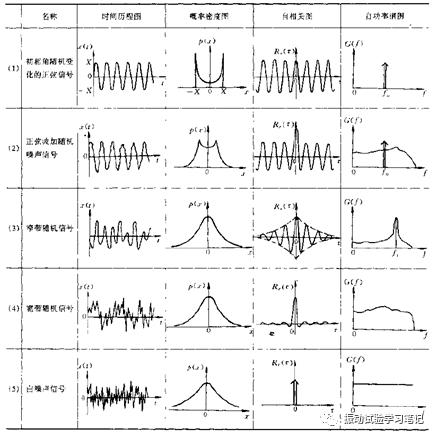
自功率谱密度函数是一个很有用的函数,描述随机振动的频率构成。x2(t)可以看成振动系统的“功和能”的度量,Rxx(τ)中含有x2(t)的成份,求出Sxx(ω)后可以得到振动能量在频率域的分布度量,因为时域和频域功率守恒(帕斯瓦定理)。
了解以上概念后,这里可以提出PSD(功率谱密度谱)的概念,在指定频率上,随机振动信号的功率谱密度为,
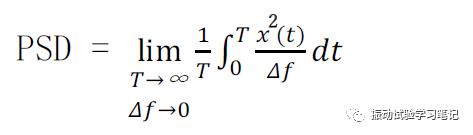
式中,可以看到在指定频率上的功率谱密度就是信号在Δf中的均方值的平均值。由于理想情况(平均时间无限长,滤波器的带宽无限窄)不可能实现,因此通常是用有限平均时间和有限带宽,即
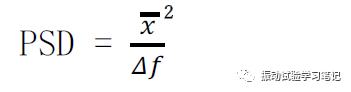
将所有的Δf和对应的PSD值连续起来,便得到了频率范围内PSD的变化形式(曲线、直线、折线等图形),这图形称为功率谱密度的频谱,也就是随机振动试验最基本的试验内容。功率谱密度的单位是g2/Hz,即单位频率上的加速度值的平方,所以在随机振动试验中也称为加速度谱密度(ASD)。功率谱密度的频谱也称为加速度谱密度的频谱。单位有g2/Hz和m2/s4二种方式,两者的关系约为100倍,即1g2/Hz = 100m2/s4。
至于PSD是怎么得到的,只要记住傅里叶变换得到的即可。具体来说,随机信号→幅值正态分布→均方值(平均功率)→帕斯瓦定理(功率守恒)→自相关函数(去除相位信息)→维纳-辛钦定理(一个信号的功率密度谱就是其自相关函数的傅里叶变换)。
(2)互功率谱密度函数Sxy(ω):它是互相关函数的傅里叶变换,其数学式如下,
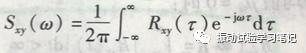
其傅里叶逆变换即
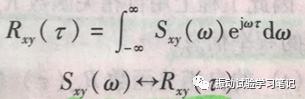
它可以用来描述两随机振动过程之间的频率信息,不仅能提供按频率分布的能量大小,还能提供两信号之间的相互关系。从互功率谱密度中,可以得到系统的频响函数,也可以确定振动响应与对其激励的时间关系。
总结:
以上说明了随机振动的4个域(时域、幅值域、时差域、频域)描述中需要的几个主要概念,对初学者来说理解起来比较困难。简单来说,对于现场随机振动,通过上面这些概念对其定义和计算,进行傅里叶变换,得到随机振动试验需要的PSD和量级。然后通过振动控制仪模拟现场随机振动试验,重现其有效频率成份(频率范围)、功率谱密度(加速度谱密度)、总均方根加速度(有效值),振动台面的运动是随机振动的时间历程,该时间历程含有现场随机振动的同样成份(频率、能量),是其典型代表,但波形基本上不是同样的。

备注:图片和部分文字等来源于网络,如有侵权,请联系作者本人。

长按二维码识别关注我们
